EWSNet. The Early Warning Signal Network
Lets anticipate critical transitions in complex systems !
What is machine learning ?
Maintaining a level of abstraction, human intelligence, and decision-making can be understood as analogies to mathematical functions . The inference that we make is essentially a function that processes a set of input sensory signals, mapping it to some meaningful target domain. For example, when one infers that is an apple, it can be understood as a function that maps visual sensory signals to a known space of objects. What constitutes knowledge and intelligence then is learning such functions, and human beings learn from experience.
On similar lines, one way to enable machines to make inferences is to model the task using a parameterized function that maps data in some input space to a desired target space. Machine 'learning' then refers to finding the optimal parameters for the function that best explains the data for the task at hand. Utilizing samples of data in the input and target spaces, one can learn the function that maps the input domain to the target domain. This enables performing inference on a new/unseen data point. This is popularly known as supervised learning and constitutes the base for the functioning of EWSNet.
What is Deep learning / Neural Networks and why use them ?
Deep neural networks are essentially parameterized functions, proven to be universal function approximators. Efficiently learning from data using classical machine learning models often required handcrafting efficient feature representations for the data. The advent of convolutional neural networks enabled stacking multiple neural network layers and going deep, to automatically extract features that are important for learning, from raw input data.
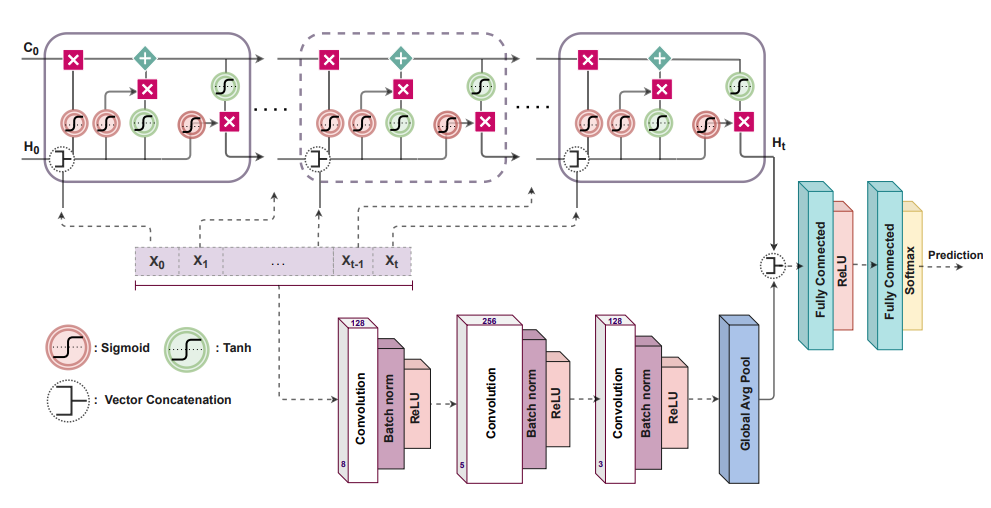
Understanding the EWSNet Architecture
In their original form, neural networks were built to process IID data samples in fixed dimensional spaces. On the contrary, most real-life data such as time-series, text, audio, video, etc., are sequential in nature and of variable length. To be able to process such sequential data and capture the inherent dependence that is present, novel neural network architectures have been proposed, the most popular among them being recurrent neural networks (RNN). RNNs process sequential data in an iterative manner, keeping a memory of data at the previous time steps. However, capturing long-term dependencies is difficult with RNNs. An LSTM is a sophisticated RNN architecture that addresses this issue by enabling the addition and deletion of information to a common memory that is propagated across time steps.
Thus, EWSNet is a parameterized function that employs an LSTM to capture long-term dependencies in the sequential time series data, in addition to a fully convolutional submodule that helps automatically extract complex non-linearities from the data, requisite to learn the characteristics indicative of a future transition.
Here you can load the time series data and visualize them prior to making predictions on them using EWSNet. We provide the following two options for generating data.
- Load some of the well studied real world time series data obtained from natural systems literature , known to exhibit a catastrophic transitions.
- Simulate stochastic time series data by varying the parameters of the differential equation. We use the Euler Maruyama method to solve the differential equation.
Load Data
You can chose to load real world data or simulate stochastic time series using the options given in pane below.
Click on the buttons provided below to load the corresponding real world data. For further details, see the references provided.